
ISC Class 12 Computer Science previous year paper (2017)
- Categories Sample Papers
Part I (20 marks)
Answer all questions.
While answering questions in this Part, indicate briefly your working and reasoning, wherever required.
Question 1 [1 mark each]
(a) State the law represented by the following proposition and prove it with the help of a truth table:
P V P = P
(b) State the Principle of Duality.
(c) Find the complement of the following Boolean expression using De Morgan’s law:
F(a,b,c) = (bʹ + c) + a
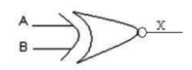
(d) Draw the logic diagram and truth table for a 2 input XNOR gate.
(e) If (~P => Q) then write its:
(i) Inverse
(ii) Converse
Ans.
(a) Law : Idempotent Law. It states that P ˅ P = P and P ˄ P = P .
Truth Table:
| P | P | P ˅ P |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
(b) Principle of Duality states that, to every Boolean Equation there exists another equation which is dual to the original equation. To achieve this, the AND’s (.) are converted to OR’s (+) and vice-versa, 0’s to 1’s and vice versa, however, the complements remain unchanged.
(c) Complement of : F( a,b,c ) = (b’ + c ) +a
= (b’ + c)’ . a’
= b’’ . c’ .a’ = b . c’ . a’
(d) XNOR gate :
| A | B | X |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
(e) If (~ P => Q ) then ;
(i) Inverse : ( P => ~ Q ) OR P’ + Q’
(ii) Converse : ( Q => ~ P ) OR Q’+ P’
Question 2 [2 marks each ]
(a) What is an interface? How is it different from a class?
(b) Convert the following infix expression to postfix form:
P * Q / R + (S + T)
(c) A matrix P[15][10] is stored with each element requiring 8 bytes of storage. If the base address at P[0][0] is 1400, determine the address at P[10][7] when the matrix is stored in Row Major Wise.
(d) (i) What is the worst case complexity of the following code segment:
for (int x = 1; x <=a; x++)
{
statements;
}
for (int y = 1; y <=b; y++)
{
for (int z = 1; z <=c; z++)
{
statements;
}
}
(ii) How would the complexity change if all the three loops went to N instead of a, b and c?
(e) Differentiate between a constructor and a method of a class.
Ans.
(a) Interface is a non primitive data type which has static and final data members and prototype of functions ( i.e. functions are not defined )
Difference : Interface supports multiple inheritance whereas a Class does not support multiple Inheritance
(b) Infix to postfix : P * Q / R + ( S + T )
= P * Q / R + ST+
= P Q* / R + ST+
= PQ*R/ + ST+
Ans : P Q * R / S T + +
(c) Row Major Wise: P[i][j] = BA + W [ (i – lr )* column + (j – lc]
= 1400 + 8[ (10-0)*10 + (7-0)]
= 1400 + 856
P[10][7] = 2256
(d) (i) O(a) + O(b x c)
= O(a + bc)
(ii) O(N) + O(N²)
= O(N²) taking the dominant term.
(e) Constructor has the same name of the class where as a method has a different name. There is no returning type, not even void in constructor where as in a method it can return a value.
Question 3 [5 marks ]
The following function magicfun( ) is a part of some class. What will the function magicfun( ) return, when the value of n=7 and n=10, respectively? Show the dry run/working:
int magicfun( int n)
{ if ( n= = 0)
return 0;
else
return magicfun(n/2) * 10 + (n % 2);
}
Ans.
(i) when n=7 OUTPUT : magicfun(7)
magicfun(3) * 10 + 1
magicfun(1) *10 + 1
magicfun(0) *10 + 1
0
= 111
(ii) when n=10 OUTPUT : magicfun(10)
magicfun(5) * 10 + 0
magicfun(2) *10 + 1
magicfun(1) *10 + 0
magicfun(0) *10 + 1
0
= 1010
PART – II (50 Marks)
Answer six questions in this part, choosing two questions from
Section A, two from Section B and two from Section C.
SECTION – A
Answer any two questions.
Question 4
(a) Given the Boolean function F(A, B, C, D) = Ʃ (2,3,4,5,6,7,8,10,11).
- Reduce the above expression by using 4-variable Karnaugh map, showing the various groups (i.e. octal, quads and pairs).
- Draw the logic gate diagram for the reduced expression. Assume that the variables and their complements are available as inputs.
(b) Given the Boolean function F(P, Q, R, S) = ππ(0,1,2,4,5,6,8,10).
- Reduce the above expression by using 4-variable Karnaugh map, showing the various groups (i.e. octal, quads and pairs).
- Draw the logic gate diagram for the reduced expression. Assume that the
variables and their complements are available as inputs.
Ans.
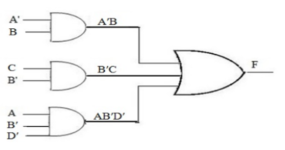
(a) F(A,B,C,D) = ∑ ( 2 , 3 , 4, 5 , 6 , 7 , 8 , 10 , 11 )

There are two quads and one pair:
Quad 1 (m2+ m3+ m10 m11 ) = B’C Quad2 ( m4+ m5+ m6+ m7 ) = A’B
Pair (m8+ m10) = AB’D’
Hence F (A, B, C, D) = B’C + A’B + AB’D’
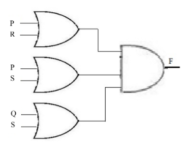
4(b) F(P,Q,R,S) = π ( 0 , 1 , 2 , 4 , 5 , 6 , 8 , 10 )
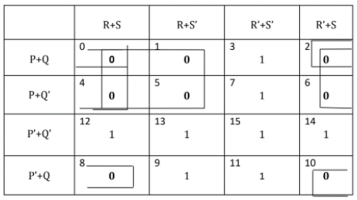
There are three quads :
Quad 1 : ( M0 M1 M4 M5) = P + R Quad 2 : ( M0 M2 M4 M6) = P + S
Quad 3 : ( M0 M2 M8 M10) = Q + S
Hence F(P,Q,R,S) = ( P + R) . (P + S) . (Q + S)
Question 5
(a) A school intends to select candidates for an Inter-School Essay Competition as per the criteria given below:
• The student has participated in an earlier competition and is very creative.
OR
• The student is very creative and has excellent general awareness, but has not participated in any competition earlier.
OR
• The student has excellent general awareness and has won prize in an inter-house competition.
The inputs are:
INPUTS
A participated in a competition earlier
B is very creative
C won prize in an inter-house competition
D has excellent general awareness
(In all the above cases 1 indicates yes and 0 indicates no).
Output : X [1 indicates yes, 0 indicates no for all cases]
Draw the truth table for the inputs and outputs given above and write the POS expression for X(A,B,C,D). [5]
(b) State the application of a Half Adder. Draw the truth table and circuit diagram for a Half Adder. [3]
(c) Convert the following Boolean expression into its canonical POS form: [2]
F(A,B,C) = ( B + Cʹ) · (Aʹ + B)
Ans.
(a)
| A | B | C | D | X (OUTPUT) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
POS Expression: X (A ,B, C, D) = π (0,1, 2, 4, 6, 8, 9, 10)
X(A ,B, C, D) = (A+B+C+D) . (A+B+C+D’) . (A+B+C’+D) . (A+B’+C+D) .
(A+B’+C’+D) .(A’+B+C+D) . (A’+B+C+D’) . (A’+B+C’+D)
(b) Application of Half Adder is to perform partial addition of two bits.
Truth table of Half Adder :
| A | B | PS | CARRY |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Circuit diagram for a Half Adder :

(c) Convert to Canonical form: F(A,B,C)=(B+C’) . (A’+B)
= (B+C’+0) . (A’+B+0)
= (B+C’+(A.A’)) . (A’+B+(C.C’))
= (A+B+C’) . (A’+B+C’) . (A’+B+C)
Question 6
(a) What is a Multiplexer? How is it different from a decoder? Draw the circuit diagram for a 8:1 Multiplexer. [5]
(b) Prove the Boolean expression using Boolean laws. Also, mention the law used at each step. [3]
F = (xʹ + z) + [ (yʹ + z) • (xʹ + y) ]ʹ = 1
(c) Define maxterms and minterms. Find the maxterm and minterm when: [2]
P = 0, Q = 1, R = 1 and S = 0
Ans.
(a) A Multiplexer is a combinational circuit which inputs parallel data and outputs one serial data where as, a Decoder is a combinational circuit which inputs n lines and outputs 2n or fewer lines.
Circuit diagram of a 8:1 Multiplexer :

(b) Prove: F = (x’+z) + [ (y’+z).(x’+y) ] ‘ =1
= (x’+z) + (y’+z)’ + (x’+y)’ ( De Morgan Law)
= x’+z + y.z’ + xy’ (Distributive Law)
= (x’+x)(x’+y’) + (z+z’)(z+y)
= x’+y’+z+y
= 1 (as y+y’=1) (Identity Law)
(c) Maxterm : It is the sum of all its literals.
Minterms : It is the product of all its literals.
When P= 0 , Q = 1 , R = 1 , S = 0
Maxterm = P + Q’ + R’ + S
Minterms = P’ Q R S’
SECTION – B
Answer any two questions.
Question 7 [marks 10]
A class Palin has been defined to check whether a positive number is a Palindrome number or not.
The number ‘N’ is palindrome if the original number and its reverse are same. Some of the members of the class are given below:
| Class name | Palin |
|---|---|
| Data members/instance variables: | |
| num | integer to store the number |
| revnum | integer to store the reverse of the number |
| Methods/Member functions: | |
| Palin( ) | constructor to initialize data members with legal initial values |
| void accept( ) | to accept the number |
| int reverse(int y) | reverses the parameterized argument ‘y’ and stores it in ‘revnum’ using recursive technique |
| void check( ) | checks whether the number is a Palindrome by invoking the function reverse( ) and display the result with an appropriate message |
Specify the class Palin giving the details of the constructor ( ), void accept( ),int reverse( int ) and void check( ).
Define the main( ) function to create an object and call the functions accordingly to enable the task.
import java.util.*;
public class Palin
{
int num,revnum;
static Scanner x=new Scanner(System.in);
Palin()
{
num=0;revnum=0;
}
void accept()
{
System.out.println( "Enter a number");
num=x.nextInt();
}
int reverse(int y)
{
if(y>0)
{
revnum =revnum * 10 + y%10;
return reverse(y/10);
}
else
return revnum;
}
void check()
{
int p=num;
if( num==reverse(p))
System.out.println("palindrome");
else
System.out.println("not a palindrome");
}
static void main()
{
Palin obj=new Palin();
obj.accept();
obj.check();
}
}
Question 8 [marks 10]
A class Adder has been defined to add any two accepted time.
Example: Time A – 6 hours 35 minutes
Time B – 7 hours 45 minutes
Their sum is – 14 hours 20 minutes ( where 60 minutes = 1 hour)
The details of the members of the class are given below:
| Class name | Adder |
|---|---|
| Data member/instance variable: | |
| a[ ] | integer array to hold two elements (hours and minutes) |
| Member functions/methods: | |
| Adder( ) | constructor to assign 0 to the array elements |
| void readtime( ) | to enter the elements of the array |
| void addtime( Adder X, Adder Y) | adds the time of the two parameterized objects X and Y and stores the sum in the current calling object |
| void disptime( ) | displays the array elements with an appropriate message (i.e. hours = and minutes = ) |
Specify the class Adder giving details of the constructor( ), void readtime( ), void addtime(Adder, Adder) and void disptime( ). Define the main( ) function to create objects and call the functions accordingly to enable the task.
import java.util.*;
public class Adder
{
int a[]=new int[2];
static Scanner x=new Scanner(System.in);
Adder()
{ a[0]=0;a[1]=0;
}
void readtime()
{
System.out.println("Enter hours and minutes");
a[0]=x.nextInt();
a[1]=x.nextInt();
}
void disptime()
{
System.out.println("Hours=" + a[0]);
System.out.println("Minutes=" + a[1]);
}
void addtime(Adder X,Adder Y)
{
a[1]=X.a[1] + Y.a[1];
a[0]=a[1]/60;
a[1]=a[1]%60;
a[0] += X.a[0] + Y.a[0];
}
static void main()
{
Adder a=new Adder();
Adder b=new Adder();
Adder c=new Adder();
a.readtime();
b.readtime();
c.addtime(a,b);
c.disptime();
}
}
Question 9 [marks 10]
A class SwapSort has been defined to perform string related operations on a word input.
Some of the members of the class are as follows:
| Class name | SwapSort |
|---|---|
| Data members/instance variables: | |
| wrd | to store a word |
| len | integer to store length of the word |
| swapwrd | to store the swapped word |
| sortwrd | to store the sorted word |
| Member functions/methods: | |
| SwapSort( ) | default constructor to initialize data members with legal initial values |
| void readword( ) | to accept a word in UPPER CASE |
| void swapchar( ) | to interchange/swap the first and last characters of the word in ‘wrd’ and stores the new word in ‘swapwrd’ |
| void sortword( ) | sorts the characters of the original word in alphabetical order and stores it in ‘sortwrd’ |
| void display( ) | displays the original word, swapped word and the sorted word |
Specify the class SwapSort, giving the details of the constructor( ), void readword( ), void swapchar( ), void sortword( ) and void display( ). Define the main( ) function to create an object and call the functions accordingly to enable the task.
import java.util.*;
public class SwapSort
{
String wrd,swapwrd,sortwrd;
int len;
static Scanner x=new Scanner(System.in);
SwapSort()
{
swapwrd="";
sortwrd="";
}
void readword()
{
System.out.println("Enter word in Upper case");
wrd=x.next();
len=wrd.length();
}
void swapchar()
{
swapwrd=wrd.charAt(len-1) + wrd.substring(1,len-1) + wrd.charAt(0);
}
void sortword()
{
char c;
for(int i=65;i<=90;i++)
{
for(int j=0;j<len;j++)
{
c=wrd.charAt(j);
if(c==i)
sortwrd += c;
}
}
}
void display()
{
System.out.println("Original word = " + wrd);
System.out.println("Swapped word = " + swapwrd);
System.out.println("Sorted word = " + sortwrd);
}
static void main()
{
SwapSort x=new SwapSort();
x.readword();
x.swapchar();
x.sortword();
x.display();
}
}
SECTION – C
Answer any two questions.
Question 10 [marks 5]
A super class Product has been defined to store the details of a product sold by a wholesaler to a retailer. Define a sub class Sales to compute the total amount paid by the retailer with or without fine along with service tax.
Some of the members of both the classes are given below:
| Class name | Product |
| Data members / instance variables: | |
| name | : stores the name of the product |
| code | : integer to store the product code |
| amount | : stores the total sale amount of the product (in decimals) |
| Member functions : | |
| product (String n, int c, double p) | : parameterized constructor to assign values to data embers name=n, code=c and amount = p displays the details of the data members. |
| void show() | : displays the details of the data members |
| Class name | Sales |
| Data members / instance variables: | |
| day | : stores number of days taken to pay the sale amount |
| tax | : to store the service tax (in decimals) |
| totamt | : to store the total amount (in decimals) |
| Member functions : | |
| Sales(…) | : parameterized constructor to assign values to data |
| void compute( ) | : calculates the service tax (@ 12.4% of the actual sale amount calculates the fine @ 2.5% of the actual sale amount only if the amount paid by the retailer to the wholesaler exceeds 30 days calculates the total amount paid by the retailer as (actual sale amount + service tax + fine) |
| void show() | : displays the data members of super class and the total amount |
Assume that the super class Product has been defined. Using the concept of inheritance, specify the class Sales giving the details of the constructor(…),void compute( ) and void show( ).
The super class, main function and algorithm need NOT be written.
public class Sales extends Product
{
int day;
double tax,totamt;
Sales( String n,int a, double b, int d)
{
super(n,a,b);
day=d;
}
void compute()
{
double f=0.0;
tax= (12.4 /100) * amount;
if(day>27)
f=(2.5/100)* amount;
totamt= amount+tax+f;
}
void show()
{
super.show();
System.out.println("No of days=" + day);
System.out.println("Sales Tax=" + tax);
System.out.println("Total Amount=" + totamt );
}
}
Question 11 [marks 5]
Queue is an entity which can hold a maximum of 100 integers. The queue enables the user to add integers from the rear and remove integers from the front.
Define a class Queue with the following details:
| Class name | Queue |
|---|---|
| Data Members / instance variables: | |
| Que[ ] | array to hold the integer elements |
| size | stores the size of the array |
| front | to point the index of the front |
| rear | to point the index of the rear |
| Member functions: | |
| Queue (int mm) | constructor to initialize the data size = mm, front = 0, rear = 0 |
| void addele(int v ) | to add integer from the rear if possible else display the message “Overflow” |
| int delele( ) | returns elements from front if present, otherwise displays the message “Underflow” and return -9999 |
| void display ( ) | displays the array elements |
Specify the class Queue giving details of ONLY the functions void addele(int) and int delele( ). Assume that the other functions have been defined.
The main function and algorithm need NOT be written.
public class Queue
{
int Que[]=new int[100];
int max,f,r;
void addele(int v)
{
if(r<max-1)
Que[++r]=v;
else
System.out.println("Overflow");
}
int delele()
{
if(f!=r)
return Que[++f];
else
return -9999;
}
}
Question 12
(a) A linked list is formed from the objects of the class Node. The class structure of the Node is given below:
class Node
{
int num;
Node next;
}
Write an Algorithm OR a Method to count the nodes that contain only odd integers from an existing linked list and returns the count. The method declaration is as follows: [2]
int CountOdd( Node startPtr )
(b) Answer the following questions from the diagram of a Binary Tree given below:
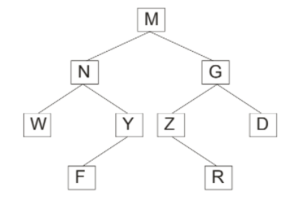
(i) Write the postorder traversal of the above tree structure. [1]
(ii) State the level numbers of the nodes N and R if the root is at 0 (zero) level. [1]
(iii) List the internal nodes of the right sub-tree. [1]
Ans.
(a) ALGORITHM:
Step 1. Start
Step 2. Set temporary pointer to the first node
Step 3. Repeat steps 4 and 5 until the pointer reaches null. Return count
Step 4. Check for odd and increment the counter.
Step 5. Move pointer to the next node
Step 6. End
METHOD:
int CountOdd(Node startPtr)
{
int c=0;
Node temp=new Node(startPtr);
while(temp != null)
{
if (temp.num % 2 != 0)
c++;
temp=temp.next;
}
return c;
}
(b) (i) W F Y N R Z D G M
(ii) Level of N=1 and Level of R=3
(iii) G and Z
You may also like

ISC Class 12 Computer Science previous year paper (2020)

